[科普中国]-μ零集

设A是测度空间(Ω,?,μ)中的可测集。如果μ(A)=0，则称A为μ零集（μ-null set）。

简介μ零集亦称μ零测度集，是测度论中的一类重要集合。

设A是测度空间(Ω,?,μ)中的可测集。如果μ(A)=0，则称A为μ零集。

性质空集是任何测度的零集；有限集和可数集是勒贝格测度的零集。1

测度论测度论是研究一般集合上的测度和积分的理论。它是勒贝格测度和勒贝格积分理论的进一步抽象和发展，又称为抽象测度论或抽象积分论，是现代分析数学中重要工具之一。 测度理论是实变函数论的基础。

测度理论是实变函数论的基础。所谓测度，通俗的讲就是测量几何区域的尺度。 我们知道直线上的闭区间的测度就是通常的线段长度； 平面上一个闭圆盘的测度就是它的面积。

可测集设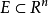，若对任意的点集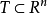，有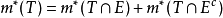，则称E为Lebesgue可测集，简称可测集。

注意事项如下：

（1）可测集的全体记为M，对于可测集E，称其外测度为测度，记为m(E)。

（2）称测度为零的可测集为零测集。空集、有限集、可数集皆为零测集。

（3）通常称定义中的条件为卡氏条件，称其中的集T为试验集。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学