[科普中国]-终归紧映射

终归紧映射是在超限迭代意义下最终可归结为紧映射的一一种映射。极限紧映射是终归紧映射的特例。

简介终归紧映射是在超限迭代意义下最终可归结为紧映射的一一种映射。

超限集列设Ω是X中的有界开集，f: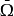→X连续。定义超限集列Rα如下：

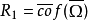
当α是第一类序数时，令。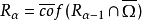

当α是第二类序数时，令。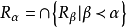

超限集列Rα是递减的，故存在某个序数α0，使得当α≻α0时，诸集Rα均相同，记之为R*。

定义若R*是紧集，则称f为Ω上的终归紧映射。1

性质如果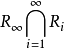是紧的，则称f为极限紧映射。极限紧映射是终归紧映射的特例。

凝聚映射是终归紧的。

若f: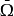→X是终归紧的（或极限紧的），则I-f称为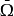上的终归紧向量场（相应地，极限紧向量场）。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院