[科普中国]-序有界

设E是有序线性空间，如果E的子集B是区间的子集，则称B是按序的意义有界。

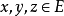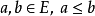简介设E是有序线性空间， 。对 ，称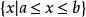 为区间，记为 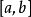。如果E的子集B是区间的子集，则称B是按序的意义有界，即序有界。

设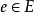 ，如果对任何 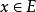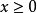， ，总存在正整数n，使 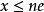，则称e为E的阿基米德单位。1

有序线性空间有序线性空间是具有序结构的线性空间。有序线性空间这个概念首先由里斯(Riesz,F.)引入，他于1928年在波隆那国际数学家大会上的讲演中奠定了半序线性空间这一泛函分析分支的理论轮廓。

设E是实线性空间，并且有序结构，即对E中某些向量对(x,y)有x≥y（或写作y≤x），“≥”满足如下条件：对任何x,y,z∈E及实数λ，

1.x≥x；若x≥y且y≥x,则x=y；若x≥y且y≥z,则x≥z。

2.著x≥y，则x+z≥y+z。

3.若x≥y，λ≥0，则λx≥λy，这时称E是有序线性空间（或称E是半序线性空间）。

里斯空间里斯空间是一类有序线性空间。

设E是有序线性空间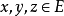，。如果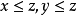，则称z是x和y的一个上界。进而，如果x和y的每个上界u都有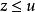，则称z是x和y的最小上界，也称为上确界或上端，记为sup(x,y)或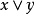。类似地可以定义x和y的下界，下确界（下端），记为inf(x, y)或。

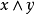如果半序线性空间E中任何两个元都有上、下确界，则称E是里斯空间，此时E对运算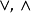封闭，故也成为格序空间或向量格。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学