[科普中国]-有限可加集函数

设μ是定义在集类?上的集函数，若对任意A,B∈?，A∪B∈?，A∩B=∅，都有μ(A∪B)=μ(A)+μ(B)，则说μ具有有限可加性。

简介设μ是定义在集类?上的集函数，若对任意A,B∈?，A∪B∈?，A∩B=∅，都有μ(A∪B)=μ(A)+μ(B)，则说μ具有有限可加性。

可列可加集函数可列可加集函数亦称完全可加集函数或可数可加集函数，是一类特殊而又重要的集函数。

若对?中任意一列互不相交的集合{An}，只要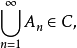均有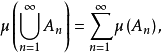则称μ具有可列可加性。

集函数集函数是测度论中定义的概念，是以集类为定义域的函数。

关于集函数，也可引入单调性、收敛性等概念。

例如，设μ是定义在集类?上的实值集函数，如果对任意A,B∈?，A⊂B，均有μ(A)≤μ(B)，则说μ在?上是单调增加的。1

本词条内容贡献者为:

武伟 - 高级工程师 - 天津直升机有限责任公司