[科普中国]-数乘变换

数乘变换(transformation of scalar multiplicalion)是一种线性变换，设V是数域P上的一个线性空间，k是P中的一个数，对任意α∈V，由σ(α)=kα所决定的线性变换σ，称为数乘变换，记为k*，这样1*就是单位变换，0*就是零变换。

基本介绍线性变换的概念设V为数域F上的线性空间，是V到V的一个映射（变换），且满足条件：

（1）对任意的α，β∈V有：

(α+β)=(α)+(β)；

（2）对任意的α∈V及任意的实数k∈F，有：

(kα)=k(α)，

则称为V的线性变换。

设V是数域F上的线性空间。定义变换为

(α)=α，α∈V，

称为恒等变换或单位变换；定义变换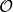为

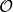(α)=0，α∈V，

称为零变换，它们都是线性变换1。

数乘变换的概念设V是数域F上的线性空间，k∈F，定义变换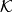 为

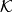(α)= kα，α∈V，

称为数乘变换，数乘变换是线性变换，故线性变换的性质也是数乘变换的性质，参见线性变换。显然当k=1数乘变换即为恒等变换，k=0数乘变换即为零变换1。

相关性质(1)设是V的一个线性变换，则：

(0)=0， (-α)=-α。

因为(0)=(0·α)=0(α)=0，

(-α)=((-1)α)=(-1)(α)=-(α)。

(2)线性变换保持向量的线性组合和线性关系式不变，即

若β是α₁，α₂，…，αs的线性组合：

β=k₁α₁+k₂α₂+…+ksαs，

则有(β)=k₁(α₁)+k₂(α₂)+…+ks(αs)，

(β)仍然是(α₁)，(α₂)，…，(αs)的线性组合，且表出系数相同。

同样若对于α₁，α₂，…，αs，有：

k₁α₁+k₂α₂+…+ksαs=0，

则有：

k₁(α₁)+k₂(α₂)+…+ks(αs)=0。

(3)线性变换把线性相关的向量组变为线性相关的向量组。

注 线性变换可能把线性无关的向量组变为线性相关的向量组，譬如零变换1。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学