[科普中国]-非线性西格玛模型

在量子场论中，非线性西格玛模型（Nonlinear sigma model）描述了一个标量场 Σ，在非线性流形中取值为目标流形T。非线性西格玛模型由Gell-Mann&Lévy于1960年引入，将其命名为对应于其模型中称为“西格玛（σ）”的无旋介子场。

内容目标流形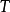配备有黎曼度量 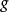，Σ是从Minkowski空间 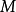（或其他空间）到 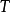的可微映射，拉格朗日密度由下式给出1：

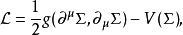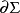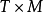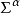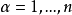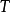使用了一个+ - - -度量标记，并且偏导数 由 射丛的一部分，V是势。在坐标表示，坐标 ， ， 是 的维度，

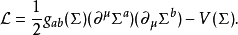
在两个以上的维度中，非线性西格玛模型包含维数耦合常数，因此不可重新规范化的。然而，它们在格子公式和Kenneth G. Wilson最初提出的双扩张中都表现出重整化群的非平凡不动点。

重整化该模型被证明与弦理论相关，Daniel Friedan提供了对其广义可重整性,他表明，该理论存在一个重整化方程组，在扰动理论的主导顺序，形式如下：

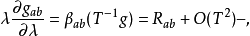
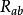是目标流形的里奇张量。

上式表示表示里奇流，遵守目标流形的爱因斯坦场方程作为固定点，这种固定点是相关的，因为它以扰动理论的顺序，由于量子校正共形场论不丢失，从而量子场理论的这个模型是可重整化的。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所