[科普中国]-改进离散余弦变换

改进离散余弦变换(Modified Discrete Cosine Transform , MDCT )是由离散余弦变换(Discrete Cosine Transform , DCT)改进而来，Princen J和Bradley A于1986年首次提出雏形，这种线性矩阵变换改善了分块变换必然存在的边界噪声，是时域混叠对消(Time Domain Aliasing Cancellation , TDAC)技术的主要组成部分。MDCT凭借其在消除边界噪声、改善信号质量方面的优越性，作为一种良好的时频分析工具，广泛应用于各种宽带高质量音频框架中。1

MDCT也是编解码系统中计算复杂度最高的三大模块之一，与一般的DCT相比，MDCT是一种非对称的变换形式。虽然它只是一种一维的变换，但其N点到N/2点、N/2点到N点的变换形式增加了算法的复杂度。MDCT是感知音频编解码标准框架中一个运算量比较大的模块，它的功能在于把编解码过程中的样本进行从时域到频域、从频域到时域的转换，以便于编码压缩处理或者是可以使信号能够实时的播放。在整个编解码系统中，它们都具有很重要的地位，是运算量最复杂的模块之一。2

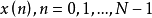给定一维序列 ，而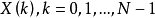 表示其变换后得到的频域序列。对于由M个采样点构成的每一个块组，可以只对M个实数值数据进行编码。因此，仍然只有M个独立的变换系数需要传输，50%重叠变换的编码性能并未降低。这里，不考虑窗函数及规一化系数，且N=2M，MDCT及其逆变换(IMDCT)简化定义为：2

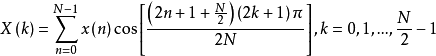
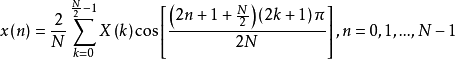
MDCT作为DCT的改进，它具有一些与离散余弦变换不同的性质：

(1) MDCT不属于正交变换，而由于其非正交特性，提高了变换效率。

(2) 不满足帕斯瓦尔定理(Parseval’s theorem)，当图3-2中输入信号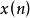 满足：

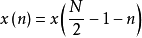
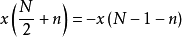n=0,1,...,N/2-1,。

MDCT得到的频域系数为零，时间域的能量不等于频域的能量。

(3)MDCT与其它的正交变换，如DFT、DCT、DST等一样，具有能量聚集的特点，可以进行频谱分析。2

在实际的硬件中，虽然MDCT的余弦函数值可以通过查表的方式来解决，但是公式内的双层嵌套循环仍然需要进行大量的计算处理，不适用于实时系统。为解决这个问题，采用了MDCT快速算法。MDCT快速算法的发展过程中，普遍采用了基于N/2点FFT、基于N/4点FFT，以及基于DCT的快速算法。

对于N点MDCT，直接实现时每个频域值需N次乘法和(N-1)次加法，总直接计算复杂度为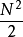 次乘法，[(N-1)×N/2]次加法。随窗口长度成平方级增加，并且需要庞大的存储块来作为查找表。

这三种算法中，基于DCT的运算量与基于FFT的运算量相当，但数据流向不规则，控制较复杂；利用N/2点FFT核计算N点MDCT时只用到了FFT变换结果的实部，造成一定的资源浪费；相对应地，采用N/4点FFT核的快速算法，则同时利用FFT复数结果的实部和虚部，提高了数据计算的效率。因而，对于2的整数次幂长度的MDCT计算普遍采用了基于N/4点的FFT。

对于N点MDCT，递归实现时每个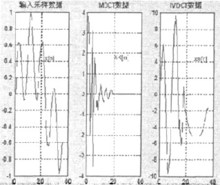频域值需N次乘法和〔N-1)次加法，总直接计算复杂度为 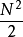次乘法，[(N-1) xN/2]次加法。随窗口长度成平方级增加，并且需要庞大的存储块来作为查找表，这不适用于实时系统。以MP3 "long“类型窗口为例，即N为36时，输入44.1khz采样的5khz和1khz双弦信号的前36个采样点为例，如图1(a)，利用MATILAB可以得到信号经过MDCT及其逆变换后的波形结果；图1(b)是N为256时的输入数据、MDCT及其逆变换结果波形，图中可以明显看出MDCT数据的低频聚集特点。但是由于直接计算运算量太大，所以具体实现中很少使用。

FFT是提出最早，应用最广泛也是最基本的快速算法。MDCT计算同其他所有DCT变换一样，因为它们的变换基核余弦函数cos(x)为指数函数exp(-jx)的实部，经过相应的预处理都可以由标准FFT算法来计算。可以采用N/2点或N/4点FFT核来实现MDCT的快速计算。然而，利用N/2点FFT核计算N点MDCT时只用到了FFT变换结果的实部，造成一定的资源浪费;相对应地，采用N/4点FFT核的快速算法，则同时利用结果的实部和虚部，提高了数据计算的利用率。

令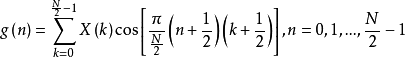

则对于 ，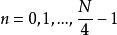

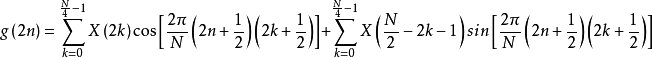
因此，输入序列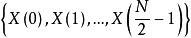 ，经过

(1) 复数序列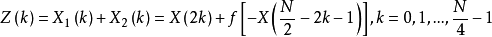： ，即次复数序列的实部和虚部分别为输入序列的偶序列和奇序列数据，并且奇序列数据倒序取反。

(2) 预旋转：

(3) N/4点FFT：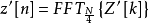

(4) 校正旋转：

四个步骤后，最后分离实部和虚部，得到N/2点数据。

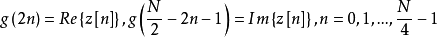
MDCT分别附加相应的预处理和后处理步骤，从而可以通过N/4点的Modified DFT(步骤2、3、4)实现了N点的MDCT。

基于FFT算法的MDCT快速算法最大的优点就是快速、效率高，基于N/4点FFT可将整个计算过程的仅需实数乘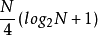法和实数加法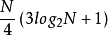。但这种算法也有自身的局限：

第一，对输入信号长度有一定的限制，如基2的FFT算法输入数据长度必须满足N=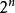，而对于MP3，规定的数据块长度N为36或12，显然不是2的整数次幂，因而不能够为MP3提供有效的算法。

第二，对资源的耗费大。FFT运算的基本单元是蝶形运算单元，1个基2蝶形运算由1个复乘和2个复加组成，而每个复乘法由2次实加法和4次实乘法完成，每个复加法由2次实加法完成，即共4次实乘法与6次实加法。由于采用同址计算，因此每个蝶形单元需要多个乘法器和加法器，若考虑到运算速度采用并列迭代或阵列处理，多个蝶形单元并行运算，资源的耗费则更多。

第三，控制较复杂。如何准确、快速的计算出地址，如何正确存取数据，如何正确控制计算流程，这些都影响着运算的正确运行，由于在FFT运算过程中需要混序或变址，以及大量的RAM、ROM，这些都使得控制较复杂。2

基于DCT算法相对比于FFT，信号能量更加集中，且只需要实数计算，这些算法都是将输入数据进行一定的预处理后，用DCT快速算法快速计算，最后再进行后处理，便可算出最终结果。

当M=N/2时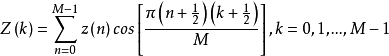，，应用三角函数的和差化积公式可得：

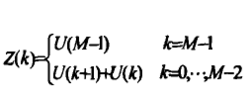
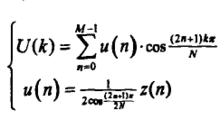
其中，n,k=0,1,...,M-1。

DCT的快速算法分为两种：间接算法和直接算法。间接算法是利用DCT和DFT、 DHT等正交变换之间的关系，用DFT或DHT快速算法来计算DCT，最初的DCT快速算法基本上都是建立在FFT基础上的。间接算法过程简单，主要工作是处理算法间的转换。直接算法包括DCT变换矩阵分解，递归算法两种技术，不同之处在于矩阵分解是利用稀疏矩阵分解法将变换矩阵分解，而递归算法是由较低阶DCT矩阵递归产生较高阶DCT矩阵，可以说递归算法是分解算法的逆算法。这里基于DCT的算法指的是基于DCT的直接算法。2