[科普中国]-LSZ约化公式

基本介绍

微观高能物理实验中，我们实际上对相互作用的细节无法测量。我们只知道反应前的粒子数（亮度）和反应后的末态数，实际表现为反应截面和衰变宽度。它们都由S矩阵元来表达。因此实际的物理观测量是S矩阵元。通过理论计算S矩阵元（用物理量如质量、耦合常数等）来表达。也就是说，通过对S矩阵元的实验测量和理论计算，我们才可以了解相互作用的本质。

那么理论计算的核心就是计算S矩阵元。历史上，Lehnamn,Symanzik和Zimmermann首先在场论框架下推导出了S矩阵元和场算符的关联函数（格林函数）的关系，现在将这种联系统称为LSZ约化公式。1相对而言，格林函数在场论中有很好的定义，是场论的更基本的物理量，包含了理论体系的所有性质。

具体而言，如果我们要计算2-body→n-body过程的S矩阵元，我们可以计算相应的n+2个Heisenberg场算符的关联函数。这些关联函数的动量空间表达在p2复空间存在极点，这些极点可以理解为对应物理态，即渐进态，它们在无穷远的过去和将来是自由的物理粒子态。多极点（比如n+2个极点）项的系数（留数）就是我们需要的S矩阵元。

不同场的约化公式标量场的LSZ约化公式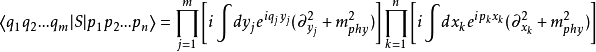

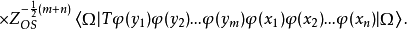
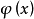：海森堡算符（相互作用理论中的算符）；

ZOS：场算符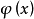 的波函数正比常数；

mphy：物理质量；

Ω：物理真空。

Dirac场的LSZ约化公式动态电子态 ：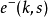

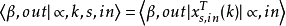
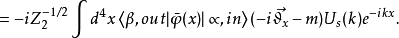
动态正电子态 ：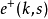

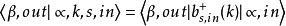
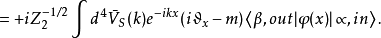
末态电子态 ：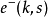

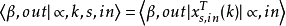
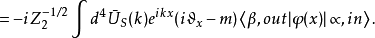
末态正电子态 ：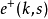

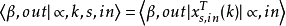
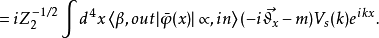
初末态包含光子的LSZ约化公式末态包含一个光子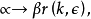

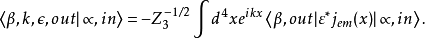
末态包含一个光子，初态包含一个光子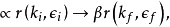

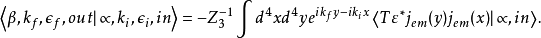
微扰论——格林函数的微扰计算在LSZ约化公式中出现的是海森堡场（相互作用场）算符关联函数（格林函数），即它们的编时乘积在物理真空态之间的矩阵元：

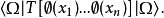
对于相互有相互作用的理论，很难对它们进行直接的解析计算。

格点场论（Lattice Field Theory）可以对它们进行数值模拟计算（采用路径积分量子化形式）。

但是，如果相互作用耦合常数比较小，相互作用Hamiltonian可以看作微扰项，则可以采用对相互作用项进行微扰展开。

格林函数在相互作用表象中（场是自由场，满足自由场运动方程）可以表示为：

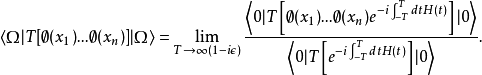
这是微扰论计算的出发点。