[科普中国]-施蒂费尔-惠特尼类

施蒂费尔-惠特尼类（Stiefel-Whitney classes）是向量丛的底空间的上同调类。

简介施蒂费尔-惠特尼类是向量丛的底空间的上同调类。

利用以下四条公理定义施蒂费尔-惠特尼类：

1、对每个实向量丛ξ都相应于一个ξ的底空间B(ξ)的以Z/2为系数的上同调类序列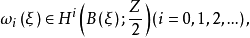称为ξ的施蒂费尔-惠特尼类。类ω0(ξ)等于单位元1∈H0(B(ξ);Z/2)，而若ξ是n-平面丛，对于大于n的i，ωi(ξ)=0。

2、自然性。若f:B(ξ)→B(η)被从ξ到η的一个丛映射覆盖，则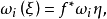f*为f诱导的同态。

3、惠特尼乘积定理。若ξ与η是同一底空间上的向量丛，则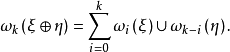

4、对于圆周P1上的典则线丛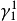，施蒂费尔-惠特尼类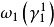不为零。

发展施蒂费尔-惠特尼类是1935年由施蒂费尔(Stiefel,E.L.)与惠特尼(Whitney,H.)定义的。而施蒂费尔-惠特尼类的公理定义是1956年由希策布鲁赫(Hirzebruch,F.E.P.)提出的。

惠特尼乘积定理属于惠特尼与吴文俊。

性质微分流形M的切丛T(M)的施蒂费尔-惠特尼类称为M的施蒂费尔-惠特尼类，记为ωi(M)(i=0,1,2,…)。1

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所