[科普中国]-谱表示定理

概念

谱表示定理是平稳随机过程相关函数的频域表达。若u(t)和y(t)是脉冲响应为h(t)、传递函数为H(s)的一个线性系统的输入和输出，则自相关函数和谱密度有以下关系：1

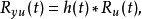
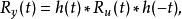
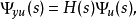
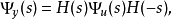其中*表示卷积，Φyu，Φy，Φu为谱密度，则有如下的谱分解定理：若对几乎每个s，|Φy(s)|≠0，则Φy(s)可惟一地分解成：

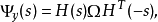
这里H(s)是一个正的实有理传递函数，其所有的极点均在左半开复平面；

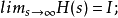
H(s)所有的极点均在左半开复平面或在jω轴上；Ω=Ω>0是实矩阵。若对所有满足Re(s)=0的s还有|Φy(s)|≠0，则H(s)的所有极点均在左半开复平面。根据(4)和谱分解定理，当输入是谱密度为Ω的白噪声时，过程y(t)可看成是稳定系统H(s)的输出，这就是谱表示定理。谱密度、谱分解定理等可用于线性随机系统。2

平稳随机过程统计特性在不同时刻平稳不变的一类随机过程。数学上严格的平稳性概念是：一随机过程，如两组时刻状态变量X(t1)，X(t2)，…，X(tn)和X(t+t1)，X(t+t2)，…，X(t+tn)的联合概率密度函数f(x(t1)，x(t2)，…，x(tn))与f(x(t+t1)，x(t+t2)，…，x(t+tn))是完全相同的(对所有的t和n)，称为平稳随机过程。一般只要求随机变量的均值和方差的平稳性，而不要求密度函数完全相等，对均值和方差保持平稳的过程，称为弱平稳随机过程或广义平稳随机过程。对水文现象，当在一定时期内，气候条件没有明显改变，流域状况和人类活动基本稳定，就认为河川年径流量和年最大洪峰流量等水文变量的变化属于平稳随机过程，不同时段观测序列求得的各种统计特征基本上是一致的。

相关函数相关函数包括自相关函数和互相关函数。其中，自相关函数是描述一个函数对于延迟一个时间的同一个函数的依赖关系。

二阶矩过程的重要数量特征。设{X(t)，t∈T}是一个二阶矩过程，定义在T×T上的二元函数R(s，t)=E(X(s)·)称为该过程的相关函数。

相关函数具有如下性质：

1.R(t，t)≥0，对所有t∈T.

2.对称性.R(s，t)=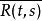 ，对所有s，t∈T.3

3.非负定性.对任意正整数n，t1，t2，…，tn∈T及任意复数λ1，λ2，…，λn，有：

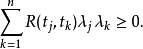
谱密度谱密度是指当信号的频带宽度趋近于零时，每单位带宽的均方根值。单位是μPa 。应当注意，谱密度只适用于具有连续谱的信号，信号的种类必须指明，例如声压、质点速度、质点加速度等。

在应用数学和物理学中，谱密度、功率谱密度和能量谱密度是一个用于信号的通用概念，它表示每赫兹的功率、每赫兹的能量这样的物理量纲。

在物理学中，信号通常是波的形式，例如电磁波、随机振动或者声波。当波的频谱密度乘以一个适当的系数后将得到每单位频率波携带的功率，这被称为信号的功率谱密度（power spectral density, PSD）或者谱功率分布（spectral power distribution, SPD）。功率谱密度的单位通常用每赫兹的瓦特数（W/Hz）表示，或者使用波长而不是频率，即每纳米的瓦特数（W/nm）来表示。

尽管并非一定要为信号或者它的变量赋予一定的物理量纲，下面的讨论中假设信号在时域内变化。4