[科普中国]-李亚普诺夫特征数

李亚普诺夫特征数是指定量描述变系数线性方程组解的稳定性态的一种数。

简介概述李亚普诺夫特征数是指定量描述变系数线性方程组解的稳定性态的一种数。

对于变系数线性方程组

其中 P(t) 在 t≥τ 上连续，李亚普诺夫引进了一些数，现在称之为李亚普诺夫特征数，来代替特征根的作用，它们是用来测定时其解的“指数”增长的数。

具体内容李亚普诺夫特征数，设φ(t) 是定义与t≥τ 上的实函数，则

为左端无穷的区间，令 为 的右端点，而

为右端无穷的区间，令 为 的左端点，如果，，都是有限的，则必有,定义这一公共值为φ 的李亚普诺夫特征数λ(φ). 如果它们之一为无穷，则λ(φ) 为无穷。

事实上

向量函数中的定义如果 为定义于t≥τ 上的向量函数，则其李亚普诺夫特征数定义为

如果矩阵 P(t) 对于大的 t 为连续有界，则：

1、变系数线性方程组（1）的每个解x(t) 的李亚普诺夫特征数λ(x) 是一个有限数

2、令 X 为变系数线性方程组（1）的所有解的集合，则数集 是一个有限集

事实上，当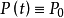 时，λ(x) 为的特征根的实部的反号数，当λ(x) 由正数构成时，变系数线性方程组 (1) 当原点为渐近稳定的。1

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学