Banach空间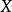 的基
的基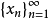 称为无条件基,如果对任何
称为无条件基,如果对任何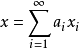 ,级数
,级数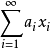 是无条件收敛的。相应地,可定义无条件基序列。
是无条件收敛的。相应地,可定义无条件基序列。
定理1 若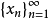 是Banach空间
是Banach空间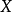 的基,则下列等价:
的基,则下列等价:
(1) 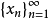 是无条件基。
是无条件基。
(2) 对正整数的每个置换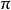 ,
,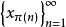 是无条件基。
是无条件基。
(3)若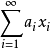 是收敛的,则对正整数集N的每个子集
是收敛的,则对正整数集N的每个子集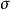 ,
,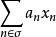 是收敛的。
是收敛的。
(4)若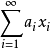 是收敛的,则当
是收敛的,则当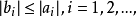 时,
时,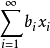 是收敛的2。
是收敛的2。
定理2 若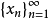 是
是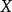 的一个无条件基(或无条件基序列),
的一个无条件基(或无条件基序列),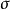 是正整数集的一个子集,定义
是正整数集的一个子集,定义
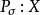 (相应地,
(相应地,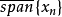 )
)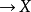 (相应地,
(相应地,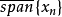 )
)
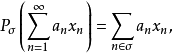 则
则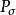 是有界线性投影。
是有界线性投影。
定义1如定理2中定义的算子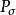 称为关于无条件基
称为关于无条件基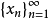 (相应地,无条件基序列)的自然投影。容易看到,当
(相应地,无条件基序列)的自然投影。容易看到,当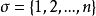 时,
时,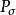 与前面定义的关于基(相应地,基序列)的自然投影是相同的。
与前面定义的关于基(相应地,基序列)的自然投影是相同的。
定理3若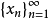 是X的一个无条件基(或无条件基序列),
是X的一个无条件基(或无条件基序列),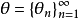 是一个符号选取(即
是一个符号选取(即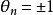 )。定义:
)。定义:
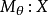 (相应地,
(相应地,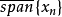 )
)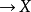 (相应地,
(相应地,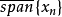 )
)
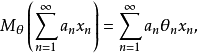 则
则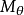 为一个有界线性算子。
为一个有界线性算子。
定理4对如上定义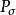 ,
,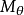 ,有下列成立:
,有下列成立:
(1) 若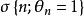 ,则
,则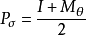 。
。
(2) 若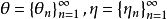 是两个符号选取,则
是两个符号选取,则
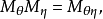 其中
其中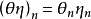 。
。
(3)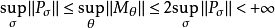 。
。
定义2若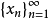 是Banach空间X的无条件基(或无条件基序列),
是Banach空间X的无条件基(或无条件基序列),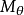 是如上定义的,则称数
是如上定义的,则称数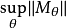 为
为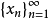 的无条件基(相应地,无条件基序列)常数。
的无条件基(相应地,无条件基序列)常数。
容易看到,无条件基常数不小于基常数。
命题1若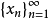 是X的无条件基,则存在X上一个等价范数,使
是X的无条件基,则存在X上一个等价范数,使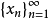 的无条件基常数等于12。
的无条件基常数等于12。
命题2若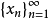 是X的一个具无条件基常数K的无条件基,则相应坐标泛函
是X的一个具无条件基常数K的无条件基,则相应坐标泛函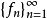 是
是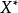 的一个无条件基序列,它具无条件基序列常数,不超过K;当
的一个无条件基序列,它具无条件基序列常数,不超过K;当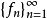 是
是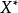 的基时,等于K。
的基时,等于K。
有了这些准备工作之后,我们开始讨论,当X具无条件基时,X将具有什么性质。
定理5若X是具有无条件基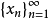 的Banach空间,则下列等价:
的Banach空间,则下列等价:
(1) 基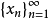 是有界完备的。
是有界完备的。
(2) X是w序列完备的。
(3) X没有闭子空间线性同胚于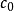 。
。
引理1若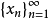 是Banach空间X的无条件基,它的无条件基常数是K,则对于使得
是Banach空间X的无条件基,它的无条件基常数是K,则对于使得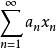 收敛的数列
收敛的数列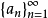 及有界数列
及有界数列 ,有
,有
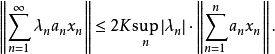 注:当X是实Banach空间时,上式的右边2K可用K来代替。
注:当X是实Banach空间时,上式的右边2K可用K来代替。
引理2若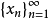 是Banach空间的无条件基,
是Banach空间的无条件基,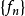 是相应的坐标泛函,若
是相应的坐标泛函,若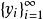 是X中一个有界序列,使对每
是X中一个有界序列,使对每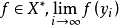 存在,且对每个
存在,且对每个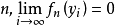 ,则
,则
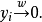
定理6若X是具无条件基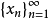 的Banach空间,则下列等价:
的Banach空间,则下列等价:
(1) 基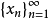 是收缩的。
是收缩的。
(2) 相应的坐标泛函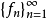 是
是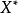 的有界完备基。
的有界完备基。
(3) 相应的坐标泛函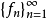 是
是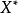 的一个基。
的一个基。
(4) 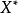 是可分的。
是可分的。
(5) X没有闭子空间线性同胚于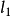 。
。
(6) 相应的坐标泛函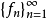 是
是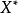 的无条件基。
的无条件基。
定理7若X是具无条件基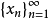 的Banach空间,则下列等价:
的Banach空间,则下列等价:
(1) X是自反的。
(2) X是w序列完备的,且X没有闭线性子空间线性同胚于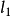 。
。
(3) X没有闭线性子空间线性同胚于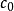 或
或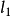 。
。
(4) 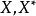 不含闭线性子空间线性同胚于
不含闭线性子空间线性同胚于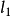 。
。
(5) 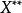 是可分的2。
是可分的2。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国