格与格论
格是有着广泛应用的一类偏序集。它是具有两个二元运算的代数系。设L是偏序集,若L的任两个元素均有上确界及下确界,则称L为格,记为(L;≤),简记为L.a,b∈L,{a,b}的上、下确界分别记为a∨b(即sup{a,b})及a∧b(即inf{a,b})。格亦可用恒等式来定义,它是由戴德金(Dedekind,J.W.R.)给出的。若代数系L有两个代数运算∧,∨,且对任意a,b,c∈L,满足下列恒等式:1
|| ||
则称L为格,记为(L;∧,∨),简记为格L。上述两种定义是等价的。1951年,索金(Sorkin,Ju.I.)用仅含三个变量的四个恒等式刻画了格;1972年,沛德迈耐罕(Padmanabhan,R.)发现可用仅含三个变量的两个恒等式刻画格,但不能用少于三个变量的两个恒等式刻画格。19世纪末,皮尔斯(Peirce,C.S.)和施罗德(Schro¨der,F.W.K.E.)在研究布尔代数的公理化以及戴德金研究代数数的理想时独立地提出了格的概念;1897年,戴德金首先对格进行了研究。在20世纪30年代中期,伯克霍夫(Birkhoff,G.D.)的著作开始了格论的全面发展,他的一系列文章展示了格论的重要性,并使格论成为代数学的一门重要分支。2
子格的概念子格是格论的基本概念之一。设S是格L的子集,若S关于L中的二元运算∧和∨是封闭的,即对任意a,b∈S,a∧b,a∨b∈S,则称S为L的子格;若子格S含0,1,则称S为格L的{0,1}-子格。若a,b∈L,a≤b,则[a,b]={x∈L|a≤x≤b}是L的子格,称为闭区间。同样可定义半开区间(a,b]和[a,b)以及开区间(a,b)。设H为格L的非空子集,L中一切包含H的子格的交,称为L的由H生成的子格,记为[H];称H为[H]的一个生成系。设S是格L的子格,若除L外,没有真包含S的子格,则称S为L的极大子格。格L的一切极大子格的交集Φ(L)称为弗拉梯尼子格。格L的所有子格按集合的包含关系构成格,记为Sub(L)。3
凸子格的定义设S是偏序集P的子集,a,b∈s,若a≤b,有[a,b]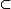 S,则称S为P的凸子集。设S是格L的子集,若a,b∈S时有[a∧b,a∨b]
S,则称S为P的凸子集。设S是格L的子集,若a,b∈S时有[a∧b,a∨b]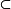 S,则称S为L的凸子格。设H是格L的非空子集,L中包含H的所有凸子格的交集仍是凸子格,称为由H生成的L的凸子格。区间、半开区间、开区间都是凸子格。4
S,则称S为L的凸子格。设H是格L的非空子集,L中包含H的所有凸子格的交集仍是凸子格,称为由H生成的L的凸子格。区间、半开区间、开区间都是凸子格。4
幂格与凸子格幂格与凸子格之间主要存在以下定义和定理:
定义1 设(L;∨,∧)是一个格,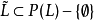 ,在
,在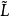 中定义运算:
中定义运算: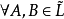 ,
,
A∨B={a∨b|a∈A,b∈B};A∧B={a∧b|a∈A,b∈B}
若(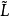 ;∨,∧)是一个格,则称
;∨,∧)是一个格,则称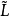 为L上的一个幂格。
为L上的一个幂格。
定义2 设(L;∨,∧)是一个格,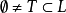 ,S是L的一个子格,若
,S是L的一个子格,若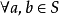 ,
,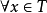 ,由a∧b≤x≤a∨b,可以推出x∈S,则称S为L的相对于T的凸子格。
,由a∧b≤x≤a∨b,可以推出x∈S,则称S为L的相对于T的凸子格。
若S是L的凸子格,则S必是L的相对于T的凸子格。
定理1 设(L;∨,∧)是一个分配格,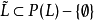 ,若
,若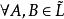 ,有A∨B∈
,有A∨B∈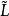 和A∧B∈
和A∧B∈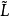 ,则(
,则(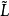 ;∨,∧)是L上的一个幂格的充要条件是存在L的一个子格T,使得:
;∨,∧)是L上的一个幂格的充要条件是存在L的一个子格T,使得:
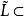 {A|A是T的非空凸子格}。
{A|A是T的非空凸子格}。
定理2 设(L;∨,∧)是一个分配格,T是L的一个子格,令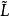 ={A|A是T的非空凸子格},则(
={A|A是T的非空凸子格},则(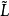 ;∨,∧)是L上的一个幂格。5
;∨,∧)是L上的一个幂格。5




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国