[科普中国]-关联公设

关联公设是图论的一个重要结论，它是电网络中基尔霍夫电流定律的推广。

简介关联公设是图论的一个重要结论，它是电网络中基尔霍夫电流定律的推广。

在系统图中，关联于任何节点的弧上的纵变量的代数和为 0 ，这个实事称为关联公设。在电网络中又称基尔霍夫电流（第一）定律，因为它是德国的物理学家基尔霍夫(Kirchhoff,G. R.)首先发现的。1

基尔霍夫电流定律基尔霍夫电流定律表明：

所有进入某节点的电流的总和等于所有离开这节点的电流的总和。

或者，更详细描述为：

假设进入某节点的电流为正值，离开这节点的电流为负值，则所有涉及这节点的电流的代数和等于零。

以方程表达，对于电路的任意节点满足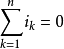：，其中， ik是第 k 个进入或离开这节点的电流，是流过与这节点相连接的第 k 个支路的电流，可以是实数或复数。

图论〔Graph Theory〕

图论是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学