闭折线边之间的交点称为自交点。自交点的个数称为自交数。
计算自交点,两边相交的算1个,三边相交的算3个,……,k边相交的算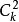 个,n边闭折线
个,n边闭折线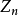 自交数记为
自交数记为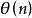 。
。
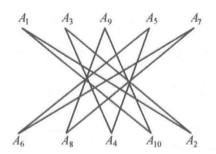
如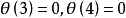 或1,在图1中,我们画出了
或1,在图1中,我们画出了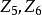 分别具有自交数
分别具有自交数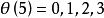 或5,
或5,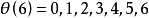 或7的一个图形。
或7的一个图形。
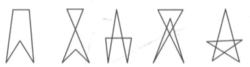
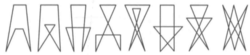
从中可以看出,0是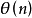 的最小值(因多边形无自交点);
的最小值(因多边形无自交点);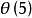 的最大值是5,相应的图形是星形,而
的最大值是5,相应的图形是星形,而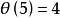 的图形没有画出;
的图形没有画出;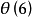 的最大值为7,相应的图形类似于6角星(但有两条双折边)。那么,
的最大值为7,相应的图形类似于6角星(但有两条双折边)。那么,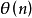 的最大值是什么呢?
的最大值是什么呢?
我们知道,n边闭折线每条边最多同其他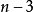 条边相交(因同它自身和两邻边不会相交),因此
条边相交(因同它自身和两邻边不会相交),因此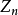 自交点最多有
自交点最多有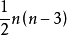 个,就是必有
个,就是必有
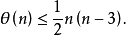
当n为奇数时,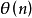 可以达到
可以达到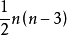 ;
;
当n为偶数时,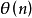 最大值为
最大值为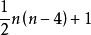 。
。
定理1 n边闭折线的最大自交数
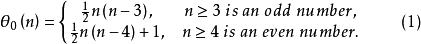
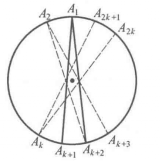
证明:事实上,当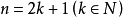 时,只需构造以正n边形最长的对角线为边的正n角星即可,如图2,在
时,只需构造以正n边形最长的对角线为边的正n角星即可,如图2,在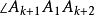 两侧,各有正n边形的
两侧,各有正n边形的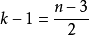 个顶点:对
个顶点:对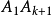 来说,其右侧还多了一个顶点
来说,其右侧还多了一个顶点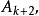 这样,就可以连出
这样,就可以连出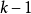 对最长的对角线(每条同
对最长的对角线(每条同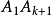 有一个交点):
有一个交点):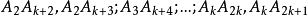 。因此,共有
。因此,共有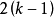 个交点,考虑所有对角线(总共
个交点,考虑所有对角线(总共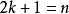 条)
条)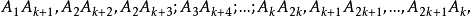 又每个交点算了两次,因此,交点总数是
又每个交点算了两次,因此,交点总数是
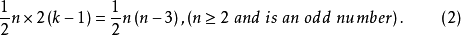
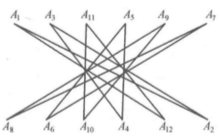
对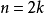 ,可用如图3所示的闭折线(图中以n=10和12为例),它顶点排列是很有规律的:奇数顶点在上,偶数顶点在下;“星形”是中心对称的。它有两条对折边
,可用如图3所示的闭折线(图中以n=10和12为例),它顶点排列是很有规律的:奇数顶点在上,偶数顶点在下;“星形”是中心对称的。它有两条对折边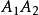 和
和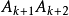 各与
各与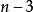 条对角线相交;其余
条对角线相交;其余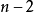 条单折边各与
条单折边各与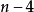 条对角线相交,而每个交点都被算了两次,因而交点的总个数为
条对角线相交,而每个交点都被算了两次,因而交点的总个数为
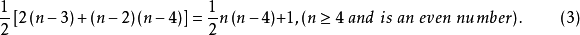
综合(2)、(3),即得(1)。
如应用调节号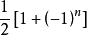 把(1)的两式合并,即得:
把(1)的两式合并,即得:
定理2 n边闭折线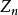 的最大自交数1
的最大自交数1
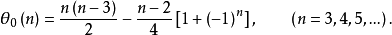




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国