[科普中国]-钝体

研究来源

空气动力学所包含的内容非常广泛，最初推动这一学科发展的巨大动力，来源于20世纪初人们想要飞的愿望。从那时起大规模的航空航天研究，以及对具有内流的机械(如喷气发动机、泵和涡轮机)所开展的研究与改进，一直在丰富着空气动力学。此外，30多年来，空气动力学在土木工程中的应用也取得新的进展，这类问题涉及的是自然风，所以主要局限于低速、不可压缩的流动现象。在应用中，空气动力学还与气象学紧密结合，特别是近地大气边界层的湍流流动。由于大多数工程结构对风表现为钝体形状，所以风工程的研究重点是钝体空气动力学。1

简介钝体是相对于流线体而言的，流线体是前圆后尖、表面光滑、略像水滴的形状。具有这种形状的物体在流体中运动时，流体沿物体的轮廓流动，基本不产生分离和尾流，因而受到的阻力最小。而对于钝体，即非流线体，在其边界上会形成流动分离，后部会产生宽阔的尾流，并伴有旋涡脱落现象(可能是周期性或非周期性)。钝体空气动力学源自于流体力学，因此其运动描述方法和控制方程与流体力学是一致的。1

钝体绕流现象边界层与流动分离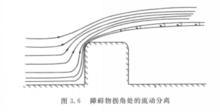在正常气压和气温下，空气的黏性很小，尽管如此，黏性对于空气流动的影响仍十分显著，特别是在靠近物体表面的区域。由于空气的黏性效应，与物体表面接触的空气贴附在物体表面，它将减慢靠近物体表面的一层空气的运动，这一空气层就称为边界层。与大气边界层中的平均风剖面类似，在边界层内，气流的速度从物体表面上为零(即无滑动)逐渐增大到边界层外的气流速度。实际上，大气边界层就是一个典型的物体边界层例子。边界层是空气黏性效应的一个重要表现。

如果边界层内的流体微粒速度因惯性力减小到使靠近物体表面的气流倒流，便出现了边界层分离。这种减速效应是因为气流中存在逆压梯度，当这种逆压梯度很大时，就会引起流动分离，例如钝体拐角的绕流就能产生这样大的逆压梯度。分离层形成离散的旋涡，并脱落到钝体后方的气流中(图1)，这些旋涡使得分离点(如拐角或房檐等)附近出现非常大的吸力。1

雷诺数效应由于空气具有质量，根据牛顿第二定律(或N-S方程)，空气除了具有黏性力外还具有惯性作用，即气流中影响最大的两个作用是黏性和惯性作用，它们的相互关系成为确定可能出现哪种类型流动特性或现象的判据，这个判据可表示为无量纲参数，即雷诺数Re，它代表了流体内的惯性力与黏性力之比。对于表面特征尺寸为 L 的某一体积气流，作用在其微团上的黏性应力可由边界层内的速度变化梯度来确定，可近似表示为μU/L，其中μ是空气的黏性系数，根据Bernoulli方程，对于速度为U的流体，惯性力近似用ρU2。来表示，这里ρ为空气密度。于是雷诺数可表示为

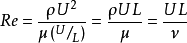
其中ν=μ/ρ为空气的分子运动黏性系数（简称动黏性系数），表征了由层流流体各层之间的分子运动所引起黏性力的大小。Re较大时，惯性效应起主要作用，反之则黏性效应起主要作用。

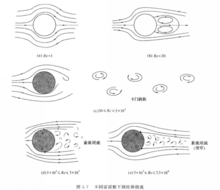下面以圆柱体为例说明雷诺数对钝体绕流的影响。如图2所示，在层流流场中，随着雷诺数从低逐渐变高，圆柱体绕流会出现多种不同的流动形态。当雷诺数很低时(Re≈1)，流体将对称地附着在整个圆周上(图2(a))。当Re≈20时，绕流形态仍是对称的，但在背风侧出现了流动分离，并形成一对始终停留在圆柱体背风侧表面附近的大旋涡(图2(b))。

当30≤Re≤5×103时，旋涡将在圆柱体两侧交替脱落，并在下游形成一条清晰稳定、交错排列的“涡迹”或“涡街”(图2(c))，这些交错排列的旋涡以略低于周围流体的速度向下游移动。由于该现象最早由冯·卡门(Von Karman)发现并解，因此被称为卡门涡街。在这一雷诺数范围内，除了旋涡本身外，圆柱体后的尾流是比较平滑而规则的，流动虽然是非定常的，但基本上可认为是层流。当雷诺数继续升高到5×103